[toc]
A linear-time algorithm for minimizing the ratio of quadratic functions over an ellipsoid
Abstract
We present a linear-time approximate algorithm for the problem(RQ)of minimizing the ratio of quadratic functions over an ellipsoid. The algorithmfrstly utilizes the bisection search to fnd a solution of Lagrange dual problemof (RQ), and then the global mimimum of (RQ) can be attained. Moreover,we prove the strong duality between primary problem and dual problem as well as give the interval of optimal Lagrange multiplier.
Introduction
we study the problem of minimizing the ratio of two quadratic functions subject to a single quadratic constraint:
$$
\begin{equation}
(\text{RQ}): \quad
\begin{array}{c l}
\min &f(x) = \displaystyle \frac{ f_1(x)}{1+ | x|^2}, \
\text{s.t.} & c(x) \leq 0,\
\end{array}
\end{equation}
$$
where $f_1(x) = x^TA_1x + 2b_1^Tx+ c_1, c(x)=x^TA_2x - c_2$ ,$A_1$ is symmetric and $A_2$ is positive semidefinite, $ b_1 \in R^n, c_1 \in R~ \text{and}~ c_2 >0 .$ In particular, the problem (RQ) includes the regularized total least squares problem (RTLS)
\begin{equation}
(\text{RTLS}): \quad
\begin{array}{c l}
\min & \displaystyle \frac{| Ax - b |^2}{1+ | x|^2}, \
\text{s.t.} & | Lx | ^2 \leq \rho.\
\end{array}
\end{equation}
Here $\rho > 0$ is a regularization parameter and $L \in R^{r\times n}$. The (RTLS) approach was extensively used in a variety of scientiflc disciplines such as signal processing, statistics, etc. Therefore, it is of great practical significance to study this (RQ) problem.
Lagrange dual frame for RQ
we first show that problem (RQ) is equivalent to solving a Lagrange dual formulation by applying strong duality.
It’s clear to see that problem (RQ) is equivalent to
\begin{equation}
(\text{RQ}): \quad
\begin{array}{c l}
\min &f(x) = \displaystyle\frac{ f_1(x)}{1+ | x|^2}, \
\text{s.t.} & \displaystyle\frac{c(x)}{1+ | x|^2} \leq 0.\
\end{array}
\end{equation}
For convenience, (RQ) problem in the following refers to above foumulation
The Lagrange function of (RQ) is writed that
\begin{equation}
L(x,\lambda) = \frac{f_1(x)}{1+ | x|^2} + \lambda \frac{c(x)}{1+ | x|^2},
\end{equation}
then the dual function is given by
\begin{equation}
g(\lambda) = \inf_x L(x,\lambda),\quad \lambda \geq 0.
\end{equation}
The Lagrange dual problem is thus
\begin{equation}
(\text{LD-RQ}): \quad
\begin{array}{c l}
\max & g(\lambda) \
\text{s.t.} & \lambda \geq 0.
\end{array}
\end{equation}
Algorithm
we utilize the bisection search to solve the Lagrange dual problem. Then, it allows us to compute a (RQ) optimal solution from a dual optimal solution.
Numerical Results
Generally speaking, we can find the optimal function value of the nonconvex problem (RQ) by firstly solving the following convex SDP problem:
\begin{equation}
(\text{SDP}): \quad
\begin{array}{c l}
\max\limits_{\lambda \geq 0} & t \
\text{s.t.} & \begin{bmatrix}
A_1 & b_1 \
b_1^T & c_1 \
\end{bmatrix} + \lambda \begin{bmatrix}
A_2 & 0 \
0 & -c_2
\end{bmatrix} \succeq tI. \
\end{array}
\end{equation}
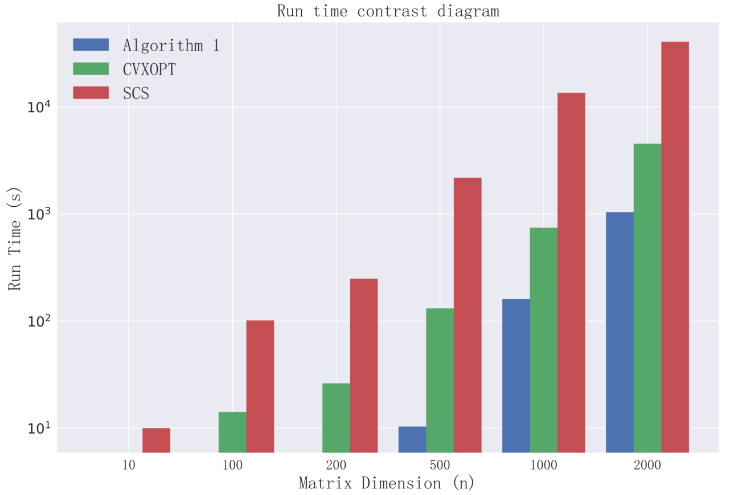
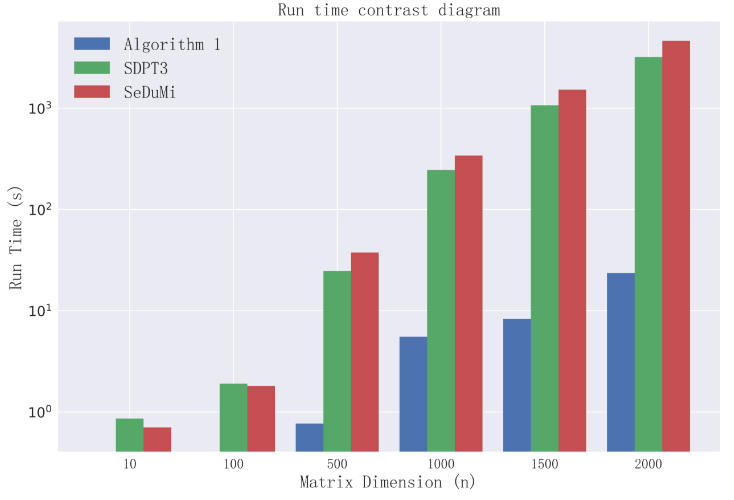
Therefore, we solve the optimal multiplier to compare the running time by some software packages and our method. These packages mainly include SeDuMi , SDPT3 within CVX as well as SCS , CVXOPT within CVXPY . Some of the experimental results are as follows.
Compare with CVX
Compare with CVXPY