[TOC]

支持向量机 vs 逻辑回归

作为面试中经常问到的一个问题，今天就从理论上作一个总结。

目标函数

一般比较SVM和LR的时候，SVM是指线性软间隔SVM，LR是加了$L_2$正则化的逻辑回归。之前详细推导过SVM和LR，两者的目标函数分别为：

SVM
\begin{equation}
\min \frac{| w |^2}{2} + C\sum_{i=1}^m \max\lbrace{ 0,1-y_i(w^Tx_i + b)\rbrace}
\end{equation}
LR
\begin{equation}
\min \sum_{i=1}^m \log \left(1+\exp\left(-y_i(w^Tx_i + b)\right) \right) + \lambda | w |^2
\end{equation}

联系

loss function 分别叫做Hinge loss和Log loss,两则都是0-1 loss的替代损失函数，从下图可以看出图片来源于《机器学习》，周志华,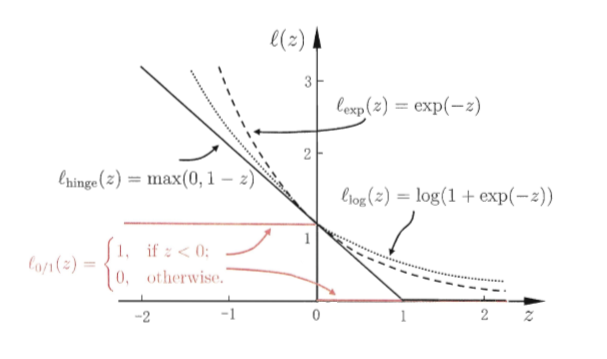 loss 两者作为替代损失，其效果其实是差不多的，当$y_i(w^Tx + b)\to 0$时，两者都趋向于0，而当 $y_i(w^Tx + b)\to - \infty$时，两者都趋向于 $-y_i(w^Tx + b)$。

区别

SVM的目标函数不可微，故无法使用基于梯度的优化算法进行求解；LR的目标函数是二阶可微的，可以使用一些基于梯度的算法直接进行求解
同样视为正则项$| w |^2$,SVM本身有着极好的几何解释（最大间隔），直接在建模的时候给出了；而LR中的正则项一般将其视为参数的先验信息，如取$L_2$范数，则视为参数服从高斯分布的先验分布，目标函数是由最大后验概率(MAP)导出.
两者的建模过程SVM是从几何的角度出发，而LR则是从统计的角度出发

概率输出

我们知道逻辑回归的输出结果，本身有着极好的概率意义，而SVM的输出却没有。一般来说，如果想让SVM的输出有概率意义，需要将SVM作一个特殊的处理，具体来说，就是需要进行三步。

SVM输出概率的步骤
step 1：找到SVM的法向量
正常的步骤求出$w_{svm},b_{svm}$
step 2：对法向量作一个伸缩变换
利用上一步得到的$w_{svm},b_{svm}$，计算数据集中的每一个样本，得到$w_{svm}^Tx_i+b_{svm}$,作为逻辑回归的输入，求解下面参数：
\begin{equation}
\sum_{i=1}^m \log\left(1+\exp\left(-y_iA(w_{svm}^Tx_i+b_{svm})+B\right) \right)
\end{equation}
step 3：转换为概率
对于每一个样本$x_i$，SVM的概率输出为：
\begin{equation}
\frac{1}{1+\exp\left(-y_iA(w_{svm}^Tx_i+b_{svm})+B\right)}
\end{equation}

核方法

SVM很容易通过其对偶问题引入核技巧，而LR就没有那么显然了。

SVM能够使用核方法的原因

首先我们分析一下SVM能够成功引入核技巧的原因：

对偶问题中出现了$\phi(x)^T\phi(x)$，在训练模型中可引入核技巧
$w$能够表示成对偶形式：$$w = \sum_{i=1}^m \lambda_iy_i\phi(x_i)$$
预测时，只需计算$$\sum_{i=1}^m \lambda_iy_i\phi(x_i)^T\phi(x_i) + b$$

如何将核方法应用到LR（KLR）

LR的目标函数中没有类似的第一点，并且由于是无约束的优化问题，也不能转化为对偶问题观察。但是，我们发现如果在LR中的w也能够表示成类似SVM的对偶形式，是不是就可以用核方法了？w能不能表示成$$w = \sum_{i=1}^m \lambda_iy_ix_i$$的形式呢？
假如我们用梯度下降法来求解LR的目标函数，回顾一下梯度下降法的更新公式：$$\theta_{k+1}=\theta_{k}-\alpha g_k,$$ 这里假设用固定的步长，$g_k$为目标函数的梯度，更直观点：
$$\theta_{k+1}=\theta_{0}-\alpha \left(\sum_{i=0}^k g_i\right)$$
回到LR问题中，LR的梯度为：
$$g=\sum_{i=1}^m \frac{\sigma(y_i(w^Tx_i+b))}{1+\sigma(y_i(w^Tx_i+b))}(-y_ix_i)+w,$$
其中$\sigma(z)=\frac{1}{1+\exp(-z)}$,利用梯度下降的更新公式，求解LR的迭代过程，实际上是对每一步的梯度方向求和，将整个过程每一项$-y_ix_i$合并，我们能够得到$$w = \sum_{i=1}^m \lambda_iy_ix_i$$这个结果，正是我们想要的。这样推导，貌似有点玄乎，实际上是有理论保证的：

定理1 对于任意一个$L_2$正则化模型
$$
\sum_{i=1}^m \text{loss} \left(-y_i(w^Tx_i + b)\right) + \lambda | w |^2
$$
最优解$w^\ast=\sum_{i=1}^m\lambda_ix_i$
证明： 从形式上看，我们就是要证明$w$落在$x_i,i=1,\cdots,m$生成的子空间中，所以可从样本生成的空间，将w分解，然后利用反证法证明w只可能在样本生成的空间中。

有了这样一个定理，我们就可以将核技巧引入到逻辑回归当中了，将w表示成上述形式，直接求解：
\begin{equation}
\min_{\beta} \sum_{i=1}^m \log \left(1+\exp\left(-y_i\sum_{j=1}^m\beta_jK(x_i,x_j)\right) \right) + \lambda \sum_{i=1}^m\sum_{j=1}^m\beta_i\beta_jK(x_i,x_j)
\end{equation}

注意上面的有些地方，我们只着重讨论$w$，而没有关注$b$，实际上这并没有什么影响，因为可以对$x$增加一个维度，将$b$合并到$w$中.

对噪声的敏感程度

先说结论：相比于LR，SVM对噪声更敏感

注意到：SVM和LR中的法向量都可以表示为 $$w=\sum_{i=1}^m\lambda_iy_ix_i,$$但是，在SVM中的推导中我们提到，SVM中的大部分$\lambda_i$都为0，只有少数$\lambda_i$不为0，与此对应的样本我们叫做支持向量，也就是说SVM中的解：$w_{svm}=\sum_{i\in S}\lambda_iy_ix_i,$,$w_{svm},$ 只与少部分支持向量有关，若SVM引入噪声，改变了支持向量，对最终的解的影响是非常巨大的，而LR的解就不具备稀疏的性质，引入少部分噪声，并不会对最终的解影响太大。

References

[1] 周志华，机器学习
[2] 林轩田，机器学习技法