[toc]
AdaBoost
算法
AdaBoost的算法思想是迭代地训练多个弱分类器$G_m(x)$,并将这多个弱分类器的结果加权组合起来作为最终的结果:
$$f(x)=\sum_{m=1}^M \beta_mG_m(x),$$
其中当迭代到第$m$次训练$G_m(x)$时,$G_m(x)$需要参考前$m-1$次的训练结果,参考的方式是根据$f_{m-1}(x)=\sum_{i=1}^{m-1}\beta_{i}G_i(x)$对每个样本预测的结果调整样本的权重,若$f_{m-1}(x)$对样本分类错误,训练$G_m(x)$时需要增大此样本的权重,使得$G_m(x)$能够对已经训练好的分类器在分错的样本上关注更多。
AdaBoost算法
:
- 初始化每个样本的权重$w_i=\frac{1}{n},i=1,\cdots,n$
- $m=1,\cdots,M$
a. 使用带权重$w^m_i$的样本训练$G_m(x)$
b. $\epsilon = \frac{\sum_{i=1}^nw_i^mI\left(y_i \neq G_m(x_i)\right)}{\sum_{i=1}^nw_i^m}$
c. $\beta_m = \frac{1}{2}\ln\frac{1-\epsilon}{\epsilon}$
d. $w^{m+1}_i = w_i^m\exp(2\beta_m I\left(y_i \neq G_m(x_i)\right))$ - $f(x)=\sum_{m=1}^M \beta_mG_m(x)$
分析
上述算法,开始训练之前每个样本的权重都是均等的,每次迭代分类器都依据当前样本的权重训练模型,然后计算出当前模型带权重的误差率$\epsilon$,$\epsilon \in [0,\frac{1}{2}),$故,$\beta_m \in (0,+\infty)$,若当前分类器将样本错分,相应地这个样本在下一轮训练的时候权重增大$\exp(2\beta_m)$倍。
推导
本小节给出上一小节算法步骤中$\beta_m \text{以及权重}w_i^m$更新的依据。
一般AdaBoost的推导步骤都理解为基于指数损失函数的前向分步加法模型(Foward Stagewise Additive Modeling),虽然据说AdaBoost最开始并不是这样提出的,直到提出5年之后才发现AdaBoost可以从前向加法模型推导解释。
指数损失函数
$$L(y,f(x))=\exp(-yf(x))$$
前向分步加法模型
定义 $f_m = \sum_{i=1}^m\beta_iG_i(x),$ 我们需要求解$\beta_i\text{和}G_{i}(x),i=1,\cdots,m$,一般我们并不是同时解出$\beta_i,G_{i}(x),i=1,\cdots,m$,而是分步地、在求得$f_{m-1}$的基础之上,再求解$\beta_m,G_{m}(x)$.
接下来,我们基于指数损失函数和前向加法模型来推导AdaBoost. 假设我们要求解的$f(x)$满足:$$f^{\ast} = \arg\min_f \sum_{i=1}^n\exp(-y_if(x_i)),$$ 而$f(x)=\sum_{m=1}^M \beta_mG_m(x)$, 利用前向分步加法模型,假设已经求得$f_{m-1},$ 下一步需要优化的目标变为:
\begin{equation}
\begin{array}{c l}
(\beta_m,G_m) & = \arg\min_{\beta,G(x)} \sum_{i=1}^n \exp\left(-y_i(f_{m-1}(x_i) + \beta G(x_i))\right) \
& = \arg\min_{\beta,G(x)} \sum_{i=1}^n \exp(-y_if_{m-1}(x_i))\exp(-y_i\beta G(x_i))) \
& = \arg\min_{\beta,G(x)} \sum_{i=1}^n w_i^m \exp(-y_i\beta G(x_i))),
\end{array}
\end{equation}
其中$w_i^m = \exp(-y_if_{m-1}(x_i)).$
上式可以分两步求解:
首先对任意的$\beta$求出$G(x)$,
$$G_m(x) = \arg\min_{G(x)} \sum_{i=1}^n w_i^m I\left( y_i \neq G(x_i) \right).$$
接下来在$G_m(x)$ 的基础上,求出$\beta_m$:
\begin{equation}
\begin{array}{c l}
\beta_m & = \arg\min \sum_{i=1}^n w_i^m \exp (-y_i \beta G_m(x_i)) \
& = \arg\min \sum_{i \in I\left( y_i = G(x_i) \right)} w_i^m e^{-\beta} + \sum_{i \in I\left( y_i \neq G(x_i) \right)} w_i^m e^{\beta},
\end{array}
\end{equation}
对上式关于$\beta$求导并等于0,得到$$\beta_m = \frac{1}{2}\ln\frac{1-\epsilon}{\epsilon}, $$
其中$\epsilon = \frac{\sum_{i=1}^nw_i^mI\left(y_i \neq G_m(x_i)\right)}{\sum_{i=1}^nw_i^m}.$
下一步样本权重的更新则变为
\begin{equation}
\begin{array}{c l}
w_i^{m+1} & = \exp(-y_if_m(x_i)) \
& = w_i^{m}\exp(-\beta_my_iG_m(x_i)) \
& = w_i^{m}\exp(2\beta_mI(y_i \neq G_m(x_i)))\exp(-\beta_m)\
\end{array}
\end{equation}
由于$\exp(-\beta_m)$与样本无关,对每个样本均有相同作用,所以忽略这一项得到$w_i^{m+1}= w_i^{m}\exp(2\beta_mI(y_i \neq G_m(x_i)))$.
损失函数分析
指数损失与对率损失函数的等价性
前文提到AdaBoost用到的损失函数为指数损失,在函数空间,我们想要得到的最优函数为:
$$f^{\ast} = \arg\min_f E_{y|x}(\exp(-yf(x))),$$
其中,
$$E_{y|x}(\exp(-yf(x))) = p(y=1|x)e^{-f(x)}+p(y=-1|x)e^{f(x)},$$
对上式关于$f$求导并令其等于0得到:
$$f(x) = \frac{1}{2}\ln\frac{p(y=1|x)}{1-p(y=1|x)},$$
或者
$$p(y=1|x)=\frac{1}{1+\exp(-2f(x))},$$
回顾一下逻辑回归,这个式子是不是和逻辑回归有几分相似?逻辑回归利用最大似然估计最后得到了以对率损失为目标函数的优化目标,这里同样可以得出相同的损失函数。统一一下后验概率得到:
$$p(y|x)=\frac{1}{1+\exp(-2yf(x))},$$
那么最大对数似然得到:
\begin{equation}
\begin{array}{c l}
\max & \sum_{i=1}^n \ln \frac{1}{1+\exp(-2y_if(x_i))}
\end{array}
\end{equation}
等价于
\begin{equation}
\begin{array}{c l}
\min & \sum_{i=1}^n \ln \left(1+\exp(-2y_if(x_i))\right) \
\end{array}
\end{equation}
上式中的损失函数即为对率损失函数。从上面的推导,我们得出,最小化指数损失函数与最小化对率损失函数是等价的!
鲁棒性分析
由上一小节,我们推导出了指数损失函数和对率损失函数的等价性,等价性成立的条件是如果我们分别从两个不同的目标函数出发,那么求出来这个完美的$f^{\ast}$是相同的,$f^{\ast}$是客观存在的完美函数,但是现实中我们拥有的样本是有限的,机器学习的目标是通过这么多有限的样本去还原、猜测$f^{\ast}$,这时候两个不同的损失函数求得的结果可能就会存在一些差异。
想一下我们是怎么利用$f(x)$做分类的?通过$\text{sign}(f(x))$来对样本分类的,若$y_if(x_i)>0,$意味着$f(x)$将$x_i$分类正确了,否则分类错误,当分类错误时,$\exp(-y_if(x_i))$具有较大的值,会给损失函数带来较大的损失,因此优化过程中求得的$f(x)$应避免这种情况发生,类似于$0-1$损失。如下图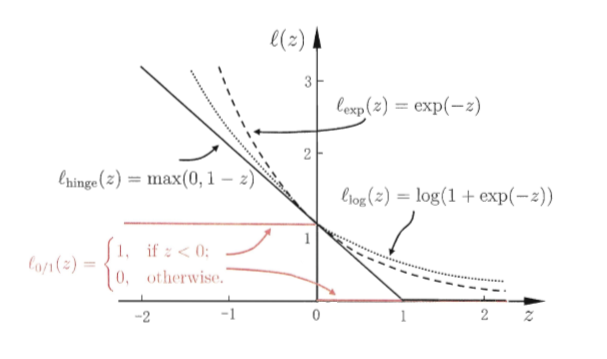
两个损失函数都是$0-1$损失的替代函数,但是它们之间存在不小的差异。
它们随$-yf(x)$变化增长的阶数不同,具体来说,一个呈指数级增长,一个为线性的。正是因为这种差异,使得对于同样的数据集,指数损失函数更倾向于优化那些使得$-yf(x)$较大的样本点,若数据中存在一些这样的点或者存在outlier将会对求得的$f(x)$具有较大影响。虽然那些$-yf(x)$较大的样本点或者outlier也会对对率损失函数产生不利影响,但是这种影响要比对指数损失函数的影响小得多。
References
[1] Hastie, The Elements of Statistical Learning
[2] 周志华,机器学习
[3] 李航,统计学习方法
