[toc]
KKT条件–约束优化问题的最优性条件
对于一些问题,利用最优性条件,往往能够求出问题的解析解,所以优化问题的最优性条件是最优化理论的重要组成部分。KKT条件是带约束问题取得最优解的必要条件(目标函数和约束可微的条件下),在某些时候可变为充要条件。
首先介绍下什么是充分条件、必要条件和充要条件:
- 充分条件:若条件C为问题P在$x^{\ast}$取得极值的充分条件,那么我们能够利用条件C直接求出$x^{\ast}$,但并不意味着所有的极值点$x^{\ast}$都满足条件C
- 必要条件:若条件C为问题P在$x^{\ast}$取得极值的必要条件,那么要想求出P的极值点$x^{\ast}$,极值点$x^{\ast}$必须满足C,但是满足条件C的点$x$却不一定是极值点
- 充要条件:满足条件C的一定是极值点,极值点一定满足条件C
本文要研究的问题的形式为:
\begin{equation}
\begin{array}{r,l}
\min & \quad f(x), x\in R^n \
\text{s.t.} & \quad c_i(x) = 0,i \in E=\left( 1,2,\cdots,l \right) \
& \quad c_i{x} \geq 0, i \in I = \left( l+1,\cdots,m \right)
\end{array}
\end{equation}
即在有等式和不等式约束的条件下极小化一个目标函数,我们记 $D=\left( x \in R^n | c_i(x)=0 , i \in E;c_i(x)\geq 0, i\in I\right)$ 为问题的可行域,$g$为$f$的一阶梯度,$G$为$f$的二阶梯度,并且我们假设目标函数和约束函数都至少是一阶可微的。
无约束优化的最优性条件
其实从形式上看,带约束的优化问题与无约束优化问题的最优性条件挺相似的,所以首先看下无约束优化问题的最优性条件,即$$\min f(x),\quad x \in R^n$$在取得极值点的时候要满足哪些条件。
定理1 一阶必要条件:若$x^{\ast}$为无约束优化问题的极小点,那么$g(x^{\ast})=0$
定理2 二阶必要条件:若$x^{\ast}$为无约束优化问题的极小点,并且$f$二阶连续可微,那么$g(x^{\ast}=0),G(x^{\ast})\text{半正定}$
举个一维函数例子: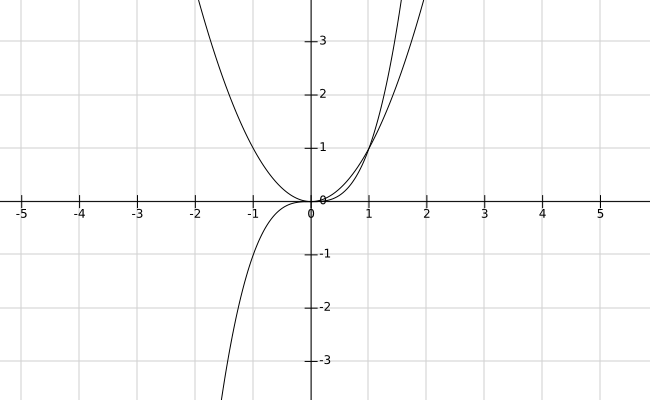
$f_1(x)=x^2, f_2(x)=x^3$,他们的一阶梯度和二阶梯度分别是$g_1(x) = 2x, g_2(x) = 3x^2,G_1(x)=2,G_2(x) = 6x$,在$x=0$处,它们分别等于$g_1(0) = 0, g_2(0) = 0,G_1(0)=2,G_2(0) = 0$,对于$f_1(x)$,它在$x=0$处满足定理1和定理2,$f_2(x)$也满足定理1和定理2,但是它并不是极值点,所以定理1和定理2只是必要条件,下面给出一个充分条件。
定理3,二阶充分条件:若$f$为二阶连续可微,并且$g(x^{\ast})=0,G(x^{\ast})$正定,则$x^{\ast}$是极小点。
对于$f_2(x)$满足定理3,所以我们断言$f_1(x)$在$x=0$处取得极小点。
等式约束的最优性条件
对于等式问题:
\begin{equation}
\begin{array}{r,l}
\min & \quad f(x), x\in R^n \
\text{s.t.} & \quad c_i(x) = 0,i \in E=\left( 1,2,\cdots,l \right)
\end{array}
\end{equation}
的最优性条件有如下定理。
定理4,等式约束的KKT条件:若$x^{\ast}$为上述问题的局部极小点,并且$f(x)$和$c_i(x)$在$x^{\ast}$的某邻域内连续可微。若$\nabla c_i(x^{\ast}),i = 1,2,\cdots,l$线性无关,则存在一组实数$\lambda_1^{\ast},\lambda_2^{\ast},\cdots,\lambda_l^{\ast}$,使得$$\nabla f(x^{\ast}) = \sum_{i=1}^l \lambda_i^{\ast} \nabla c_i (x^{\ast})$$
证明:略。
此定理为等式约束问题取得最优解的一阶必要条件,令等式约束问题的Lagrange函数为
$$L(x,\lambda) = f(x) - \sum_{i=1}^{l} \lambda_i c_i (x),$$
此定理表明,等式约束问题的最优解和最优Lagrange乘子为Lagrange函数的驻点:
\begin{gather}
\begin{pmatrix}
\nabla_x L(x^{\ast},\lambda^{\ast}) \
\nabla_{\lambda} L(x^{\ast},\lambda^{\ast})
\end{pmatrix} = 0
\end{gather}
不等式约束问题的最优性条件
对于不等式约束问题
$$
\begin{equation}
\begin{array}{r,l}
\min & \quad f(x), x\in R^n \
\text{s.t.} & \quad c_i(x) \geq 0, i \in I = \left( l+1,\cdots,m \right)
\end{array}
\end{equation}
$$
首先来看三个引理。
三个引理
引理1,Fakas引理:设$a_1,a_2,\cdots,a_r,b$为n维向量。所有满足$a_i^Td>0,i = 1,2,\cdots,r$的向量d,同时满足$b^Td>0$的充要条件是存在非负实数$\lambda_1,\lambda_2,\cdots,\lambda_r$使得$b = \sum_{i=1}^r \lambda_i a_i.$
证明:略。
可以这样理解这个引理,$d$与所有的向量$a_i$成锐角,所有的$d$生成了一个多面锥,向量b若要与这样的一个d也成锐角,那么b应该在由向量$a_i$生成的凸锥包中。
引理2,Gordan引理:设$a_1,a_2,\cdots,a_r$为n为向量,则不存在向量$d\in R^n$使得
$$a_i^Td<0,i = 1,2,\cdots,r$$
的充要条件是,存在不全为0的非负实数组$\lambda_i,i= 1,2,\cdots,r$使得
$$\sum_{i=1}^r \lambda_i a_i = 0.$$
证明: 略,需要用到Fakas引理。
这个定理的几何意义是:假设在一个平面内,如果把$a_i$看成力的话,不存在$d$,使得$a_i^T d<0$表明所有力的方向不可能都在一个180度内,那么总是可以适当对每个力进行放缩,使得合力为0.
给出一个有效约束的概念。
有效约束:对于所有的不等式约束,$\hat{x}$的有效约束是指那些在$\hat{x}$的某邻域内使得 $c_i(\hat{x}) = 0 $ 的约束,也就是说对于某些约束,$\hat{x}$已经走到了边界上,这些约束对$\hat{x}$起了作用,而那些$c_i(\hat{x})>0$的约束,$\hat{x}$还在内部,暂时还没起约束作用。
有效集:所有在$\hat{x}$处的有效约束的下标组成的集合
$$I(\hat{x}) = \lbrace i | c_i(\hat{x}) = 0\rbrace.$$
引理3: 对于不等式约束优化问题,$x^{\ast}$为优化问题的局部极小点,$I^{\ast} = \lbrace i | c_i{x^{\ast}} = 0,i=1,2,\cdots,m \rbrace$,若$f(x)$和$c_i(x_i)(i \in I^{\ast})$在点$x^{\ast}$可微,且 $ c_i(x),(i \in I/ I^{\ast}) $在点$x^{\ast}$连续,则在点$x^{\ast}$的下降方向集S与可行方向集G的交集是空集。$S = \lbrace p\in R^n | \nabla f(x^{\ast})^Tp <0\rbrace,$ $ G = \lbrace p\in R^n | \nabla c_i(x^{\ast})^Tp >0, i \in I^{\ast} \rbrace$
证明:反证法。假设存在一个向量$p \in S \cap G,$ 即$p$既是下降方向,又是可行方向,那么存在一个$\epsilon$使得$f(x^{\ast}+\epsilon p)<f(x^{\ast})$,与$x^{\ast}$为局部极小点矛盾。
Fritz-John一阶必要性条件
定理5,Fritz-John一阶必要性条件:设$x^{\ast}$为不等式约束优化问题的局部极小点,且$f(x),c_i(x)$在$x^{\ast}$点可微,则存在不全为0非零实数$\lambda_0^{\ast},\lambda_1^{\ast},\cdots,\lambda_m^{\ast}$使得
\begin{equation}
\begin{cases}
\lambda_0^{\ast} \nabla f(x^{\ast}) - \sum_{i=1}^m \lambda_i^{\ast} \nabla c_i(x^{\ast}) = 0, \
\lambda_i^{\ast} c_i(x^{\ast}) = 0,\quad \lambda_i^{\ast} \geq 0,i = 0,1,\cdots,m
\end{cases}
\end{equation}
证明: 设$x^{\ast}$处的有效集为$I^{\ast}$,由引理5知,不存在$d \in R^n,$使得$$ \nabla f(x^{\ast})^Td <0, \quad -\nabla c_i(x^{\ast})^Td <0, i \in I^{\ast},$$再由Gordan引理可得,存在不全为0非零实数$\lambda_0^{\ast},\lambda_i^{\ast},i \in I^{\ast}$使得$\lambda_0^{\ast} \nabla f(x^{\ast}) - \sum_{i \in I^{\ast}} \lambda_i^{\ast} \nabla c_i(x^{\ast}) = 0,$ 另外,规定$i \in I/I^{\ast}$时,$\lambda_i^{\ast}=0, $则得到定理结论。
KKT一阶必要性条件
Fritz-john一阶必要条件有一个缺点,就是当$\lambda_0^{\ast}= 0 $时,目标函数的梯度将从等式中消失,所以需要加一些条件使得目标函数的梯度前面的系数不为0,这样就得到了不等式约束优化问题的KT条件。
定理6,不等式约束的KKT条件:设$x^{\ast}$为不等式约束优化问题的局部极小点,且$f(x),c_i(x)$在$x^{\ast}$点可微,有效集为$I^{\ast}$, 若$\nabla c_i(x^{\ast})(i \in I^{\ast})$线性无关,则存在不全为0非零实数$\lambda_1^{\ast},\cdots,\lambda_m^{\ast}$使得
\begin{equation}
\begin{cases}
\nabla f(x^{\ast}) - \sum_{i=1}^m \lambda_i^{\ast} \nabla c_i(x^{\ast}) = 0, \
\lambda_i^{\ast} c_i(x^{\ast}) = 0,\quad \lambda_i^{\ast} \geq 0,i = 1,\cdots,m
\end{cases}
\end{equation}
证明:由Gordan引理,存在不全为0的非负数$\mu_0,\mu_i,i \in I^{\ast}$使得
$$\mu_0^{\ast} \nabla f(x^{\ast}) - \sum_{i \in I^{\ast}} \mu_i^{\ast} \nabla c_i(x^{\ast}) = 0,$$
若$\mu_0^{\ast}=0,$则$\sum_{i \in I^{\ast}} \mu_i^{\ast} \nabla c_i(x^{\ast}) = 0,$与$\nabla c_i(x^{\ast})(i \in I^{\ast})$线性无关矛盾。故上式两边同时除以$\mu_0^{\ast}$可得结论。
一般约束问题的最优性条件
结合等式约束与不等式约束优化问题的KT条件很容易得到一般约束优化问题的最优性条件。
KKT条件
\begin{equation}
\begin{cases}
\nabla f(x^{\ast}) - \sum_{i \in I} \lambda_i^{\ast} \nabla c_i(x^{\ast}) - \sum_{i \in E}\mu_i^{\ast} \nabla c_i(x^{\ast})= 0, \
\lambda_i^{\ast} c_i(x^{\ast}) = 0,c_i(x^{\ast}) \geq 0, \lambda_i^{\ast} \geq 0,\quad i \in I \
c_i(x^{\ast})=0,\quad i\in E
\end{cases}
\end{equation}
$\lambda_i^{\ast} c_i(x^{\ast}) = 0, (i \in I)$又叫做互补松弛条件。
References
[1] 倪勤,最优化方法与程序设计
