预备知识
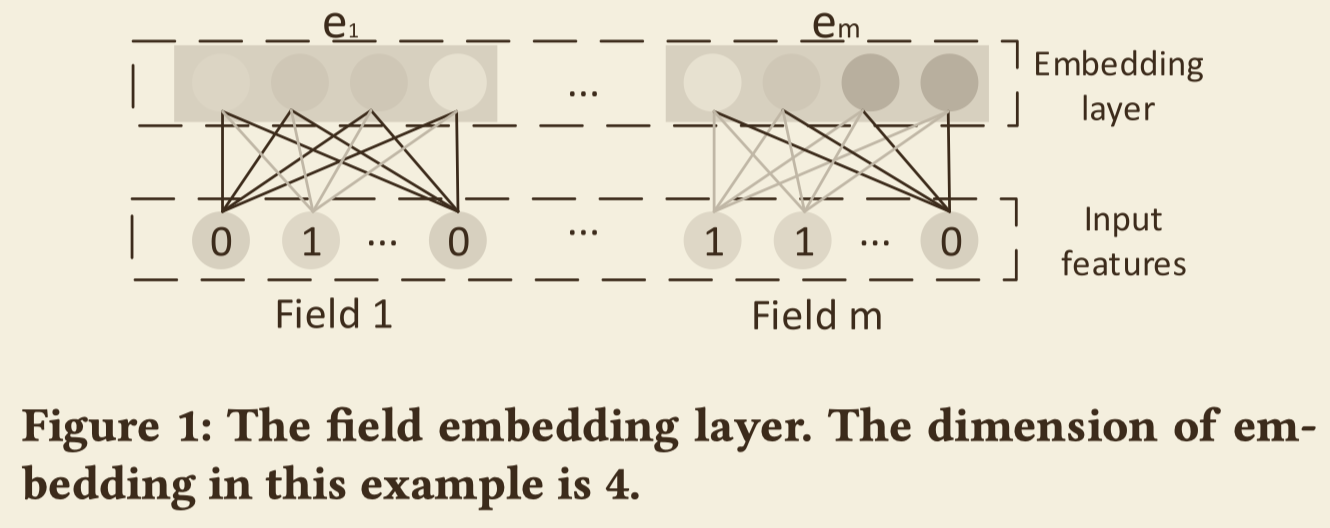
嵌入层
一般我们会对离散特征进行热编码,比如论文中给的例子:

使用FM可以为每一个特征(热编码后的)学习一个隐向量(假设每个隐向量都固定维度D),因为一个field(热编码前的特征)包含多个编码,所以每一个field就包含多个隐向量。对于一个样本,每一个field只有一个或几个隐向量出现,即热编码后特征为1的特征的隐向量,若field中只有一个隐向量出现,那么这个特征的隐向量就作为field的隐向量,若有多个隐向量出现,多个隐向量的和作为field的隐向量。
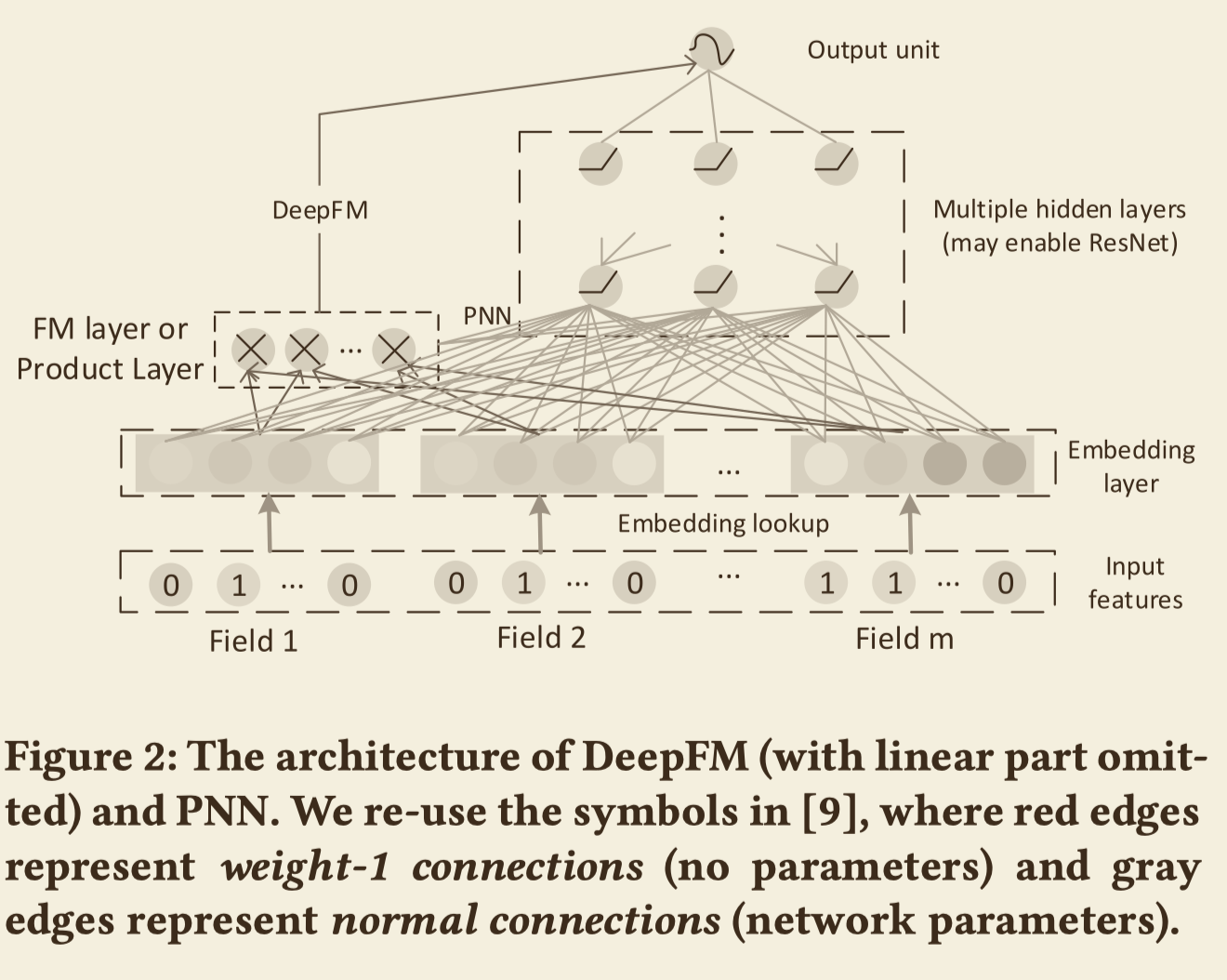
隐式高阶交叉特征
由DNN学习到的特征就叫做隐式的高阶交叉特征(Implicit High-order Interactions),如下图,DeepFM和PNN的结构画在了一起,两者都可以学习到低阶特征和隐式的高阶特征,但他俩的区别在于DeepFM是用FM层学习低阶交叉特征,PNN用product层学习低阶交叉特征。
显式高阶交叉特征
CrossNet能够学习到显式高阶交叉特征(Explicit High-order Interactions),它的网络结构如下图,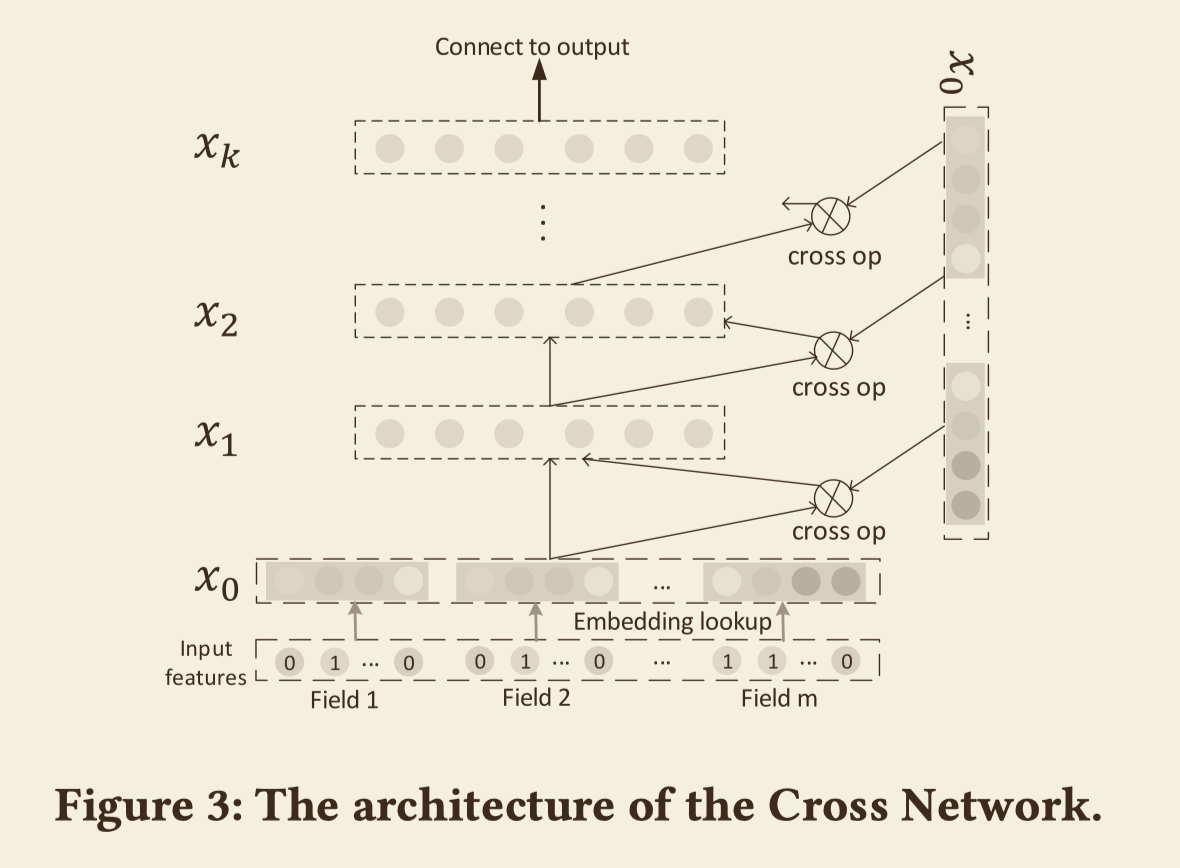
网络之间的传播公式为
$$x_k = x_0x_{k-1}^Tw_k + b_k + x_{k-1}$$
本文提出的CIN的结构就借鉴了CrossNet的网络结构。
本文方法
CIN(Compressed Interaction Network)
CIN考虑:
- 向量级别的特征交互
- 显式的高阶特征交互
- 网络的复杂度不能随着交叉的阶数指数增长
CIN的网络结构可以种下列三个图解释: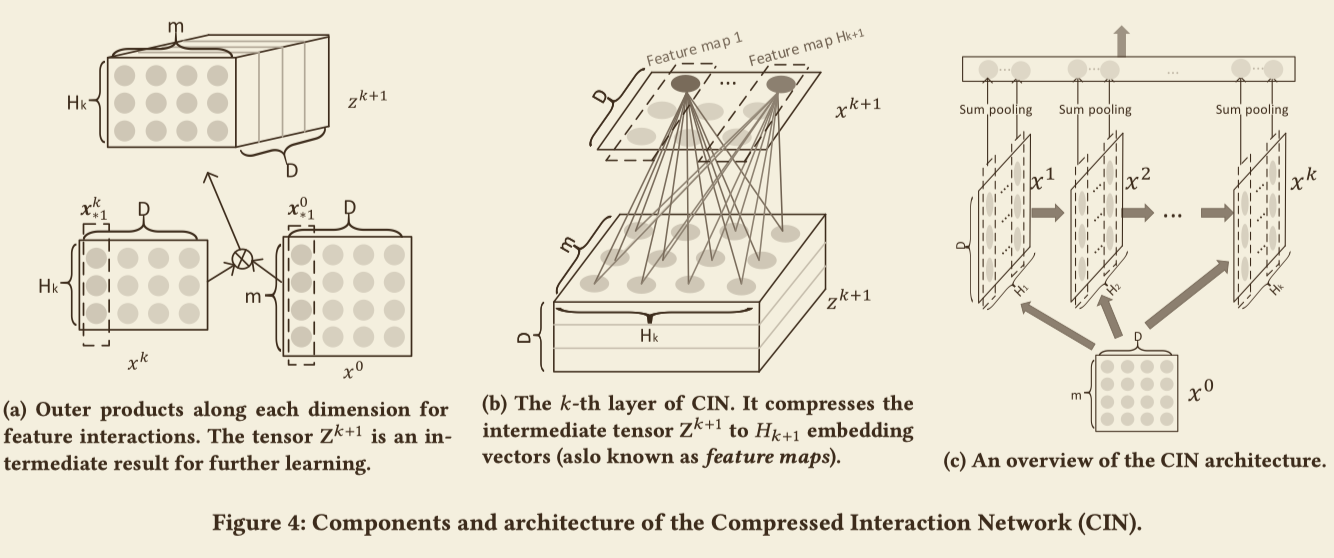
如(c)图所示,网络的输入为field的嵌入,并且用矩阵$X^0 \in R^{m\times D}$表示,其中m表示field的个数,D表示嵌入的维度,它的第i行即为第i个field的嵌入。网络的输出用$X^k \in R^{H_k\times D}$表示,$H_k$表示第k层特征向量的个数。网络之间的传播公式为
$$
X_{h,\ast}^k = \sum_{i=1}^{H_{k-1}} \sum_{j=1}^m W_{i,j}^{k,h}(X_{i,\ast}^{k-1}\circ X_{j,\ast}^{0})
$$
$\circ$的定义为$(a,b,c)\circ(x,y,z)=(ax,by,cz)$。由于下一个隐藏层的输出依赖于上一个隐藏层的输入,所以CIN的结构与RNN非常类似。
从上面的传播公式还能够看出CIN还有类似CNN的结构,如上图(a)所示,$x^k$的一列($H_k=3$维)与$x^0$的一列($m=4$维)作用可以生成一个$3*4$的矩形,总共有D列,所以最终生成了D个这样的矩形,也就是一个$H_k \times m \times D$维的tensor,所生成到每个矩阵的权重矩阵$W^{k,h}$可以视作一个滤波器,最终如图(b)所示,每个生成的 $H_k \times m$ 矩阵映射为一个 $H_{k+1}$ 维向量。
假设CIN有T个隐藏层,每个隐藏层的$X^k$的行向量都做一个sum pooling:
$$p_i^k = \sum_{j=1}^DX^k_{i,j}$$,最终能够得到一个pooling后的向量,$p^k = [p^k_1,\cdots,p^k_{H_k}]$,正如图(c)的输出层所示,T个这样的隐藏层的输出单元即为$p^+ = [p^1,\cdots,p^T]$.如果使用CIN直接只用作二分类,则输出单元可以为
$$
y = \frac{1}{1+\exp(p^+Tw^o)}
$$
CIN分析
空间复杂度
CIN共包含$\sum_{k=1}^T H_k \times H_{k-1} \times m + \sum_{k=1}^T H_k$个参数
时间复杂度
$O(mHD+H^2T)$
多项式近似
假设每一层特征映射的维度都为m。第一层第h个特征映射:
$$x^1_h = \sum_{i,j}^m W_{i,j}^{1,h}(x_i^0\circ x_j^0),$$
可以看出这是一个二阶特征交叉。第二层的第h个特征映射为:
$$
\begin{array}{c l}
x^2_h &= \sum_{i,j}^m W_{i,j}^{2,h}(x_i^1\circ x_j^0),\
&= \sum_{i,j}^m \sum_{l,k}^m W_{i,j}^{2,h}W_{l,k}^{1,i}(x_l^0 \circ x_k^0 \circ x_j^0)
\end{array}
$$
容易看出这是输入特征的3阶特征交互。能够推出第k层的特征为输入特征的k+1阶特征交互,这也叫做CIN的显示高阶特征交互的特性。
与隐式网络的组合
DNN能够学习出隐式高阶特征,所以DNN与CIN再加上线性模型就一起构成了xDeepFM,如下图所示即为xDeepFM的结构。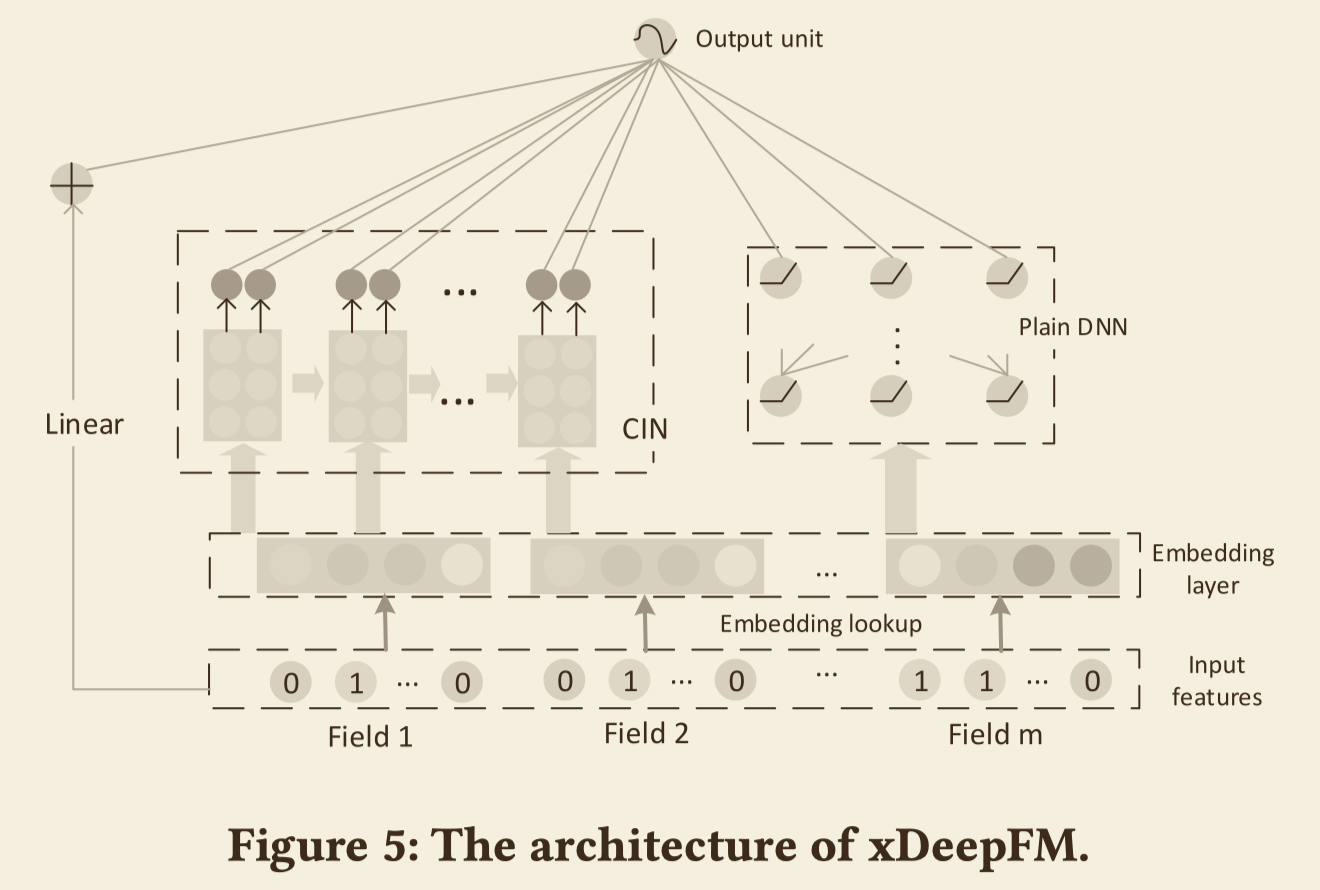
整个xDeepFM的输出单元为
$$
\hat{y}=\sigma(w_{linear}^Ta + w_{dnn}^Tx_{dnn}^k+w_{cin}^Tp^+ + b)
$$
损失函数为
$
L = -\frac{1}{N}\sum_{i=1}^N \lbrace yi \log\hat{y}i + (1-yi) \log(1-\hat{y}i)\rbrace +\lambda^{\ast}\Vert\Theta \Vert
$
后面一项为正则项。

