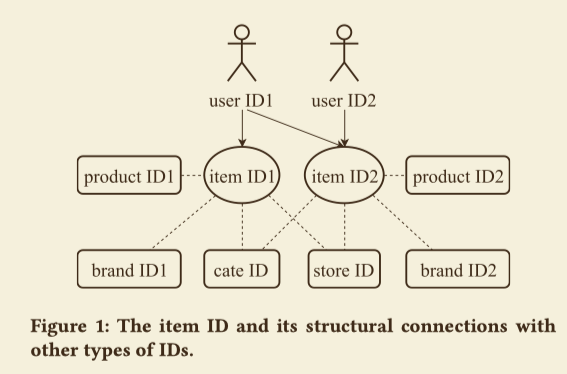
除了用户的隐式反馈,论文还考虑了不同ID类特征之间的连接结构,通过这些连接,在ItemID序列中的信息可以传播到其它类型的ID特征,并且可以同时学习这些ID特征的表示,如下图
hema 的推荐框架
这篇论文是应用在盒马鲜生这个APP中的,在这个APP中,推荐的过程主要分为4个过程:
- 准备阶段:离线计算出user-to-trigger和trigger-to-item的评分,并且把结果存储在数据库中。
- 匹配:首先根据用户的ID取出他们的
triggers,然后基于这些triggers产生一些items的推荐候选集。 - 筛选:移除无效和重复的
items. - 排序:综合一些评分指标,给这些筛选后的
items排序。
学习IDs的表示
用户交互序列的Skip-gram模型
将用户的一个交互会话视作一个documents,形式上来讲就是,给定一个item IDs ${ item_1,\cdots,itme_i,\cdots,item_N },$skip-gram模型最大化:
$$
J = \frac{1}{N} \sum_{n=1}^N \sum_{-C\leq j \leq C}^{1 \leq n+j \leq N} \log p(item_{n+j}| item_n)
$$
C是上下文窗口的长度。比如文中给的例子,每个用户都有一个序列,第一个用户的梨子就是上面公式中的$item_n$:

在基本的skip-gram模型中,$p(item_{j}| item_i)$是由softmax函数定义的:
$$
p(item_{j}| item_i) = \frac{\exp(e^{‘T}_je_i)}{\sum_{d=1}^D\exp(e^{‘T}_de_i)}
$$
其中$e^{‘} \in E^{‘}\subset R^{m\times D}, e \in E\subset R^{m\times D}$.$E^{‘},E$分别是与上下文和目标相关的表示矩阵。$m,D$是分别是嵌入向量的维度和包含所有item IDs字典的大小。
Log-uniform 负采样
上式中计算$\nabla p(item_{j}| item_i)$的时间复杂度与D成正比,当D很大的时候,上面的模型很难实际使用。所以这篇论文使用负采样的方法代替softmax函数:
$$
p(item_{j}| item_i) = \sigma(e^{‘T}_je_i) \Pi_{s=1}^S \sigma(-e^{‘T}_se_i)
$$
负样本是从$P_{neg}(item)$的分布采样得到,$P_{neg}(item)$最简单的选择是均匀分布,但是对于样本不均衡的情况下,均匀分布并不是一个好的选择,因为往往流行的item IDs都提供了很少的信息,这样的样本在目标样本的上下文窗口中出现多次却提供较少信息,这篇论文中选择了Zipfian分布作为$P_{neg}(item)$.
$$
p(index) = \frac{\log(index+2) - \log(index+1)}{\log(D+1)}
$$
首先根据items的频率按照降序排序,然后每个item都对应着一个index,index的范围从0到D-1。累积概率分布为
$$
\begin{align}
F(x) &= p(x \leq index) \
&= \sum_{i=1}^{index} \frac{\log(i+2) - \log(i+1)}{\log(D+1)} \
&= \frac{\log(index +2 )}{\log(D+1)}
\end{align}
$$
令$F(x)=r$,r为$(0,1]$之间的一个随机数,那么我们可以随机抽到一个index为
$$
index = \lceil (D+1)^r \rceil - 2.
$$
IDs 以及他们他们之间的结构连接
Item ID 以及它的属性IDs
item是交互的核心单位,它有许多属性id,包括product id,store id,brand id,category id等。
User ID
属性IDs的联合嵌入
论文提出了一个层次化的嵌入模型,去联合学习item ID以及它们的属性ID之间的低维表示,如下图
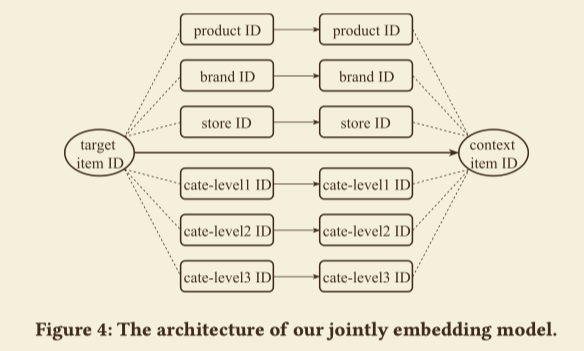
假设K类IDs,令$IDs(item_i) = [id_1{item_i},\cdots,id_K(item_i)]$,那么可以得到
$$
p(IDs(item_j) | IDs(item_i))
= \sigma \big(\sum_{k=1}^K (w_{jk}e^{‘}{jk})^T(w{ik}e_{ik})\big) \Pi_{s=1}^S\sigma \big(-\sum_{k=1}^K(w_{sk}e^{‘}{sk})^T(w{ik}e_{ik})\big)
$$
其中 $ w_{ik} $ 为 $ id_{i}( item_{i}) $ 的权重,计算方法为:
$$
w_{ik} = \frac{1}{\sum_{j=1}^D I(id_k(item_i) = id_k(item_j))}
$$
定义
$$
p(item_i|ID(item_i)) = \sigma \big( \sum_{k=2}^K w_{ik}e^T_{i1} M_k e_{ik} \big),
$$
其中$M_k \in R^{m_1 \times m_k}(k=2\cdots K)$是为了使$e_{i1}$变换到$e_{ik}$相同维度的矩阵。然后最大化
$$
J = \frac{1}{N} \sum_{n=1}^N \big( \sum_{-C\leq j \leq C}^{1 \leq n+j \leq N,j\neq 0} \log p(IDs(item_{n+j})| IDs(item_n)) + \alpha \log p(item_n| IDs(item_n)) - \beta \sum_{k=1}^K \Vert M_k \Vert_2 \big)
$$
这种方法将Item ID 和属性ID 嵌入到一个同语义空间。
嵌入用户ID
使用简单平均法:
$$
Embedding(u) = \frac{1}{T} \sum_{t=1}^T e_t
$$
$e_t$是$item_t$的嵌入向量。
利用ID的表示
item相似性度量
$$
sim(item_i,item_j) = cos(v_i,v_j) = \frac{v_i^Tv_j}{\Vert v_i \Vert_2\Vert v_j \Vert_2}
$$
从已知item迁移到未知item
为了解决冷启动问题,论文提出了一个迁移方法,对新的item ID构建一个近似的嵌入向量。因为即使是一个新的item ID,通常它的属性id也有历史记录,论文的想法是最大化概率
$$
\max p(item_i | IDs(items_i))
$$
也就是令
$$
p(item_i | IDs(items_i)) \rightarrow 1
$$
所以令
$$
e_{i1} = \sum_{k=2}^K w_{ik}e^T_{i1} M_k e_{ik}
$$
实际中只使用那些有历史记录的$id_k$.
从不同的领域迁移
本节讲了如何从淘宝用户喜好迁移到盒马平台。
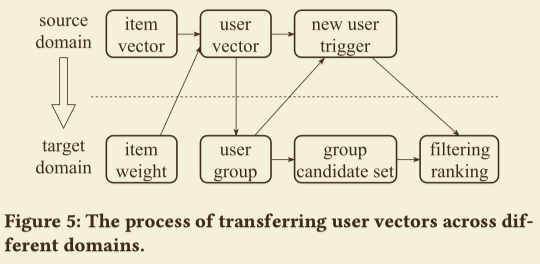
$U^s,U^t$分别表示source domain和target domain的用户集合,$U^i = U^s \bigcap U^t$。如上图所示,迁移的过程为
- 在淘宝计算出$U^s$的嵌入向量
- 基于嵌入向量的相似度,$U^i$中的用户使用k-means聚类为1000个组
- 对于每个组,选择出 top N 个盒马中的item作为候选集
- 根据相似性度量,将新用户分配到最相近的组中
- 新用户被分配到组中后,组里使用第3步选出来的候选集筛选排序后推荐给他
迁移到不同的任务
可以使用嵌入向量和历史销售作为输入做销售预测任务,使用的模型为全连接神经网络。
