listing embedding
这里的listing应该是一个item。假设$s = (l_1, l_2, \cdots,l_M) \in S$是一个用户点击listing的序列,其中S是表示所有用户点击序列的集合,给定这样一个序列集合,我们的目标是学习每个$l_i$的一个d维嵌入,为了学习这样一个嵌入表示,论文借鉴了skip-gram模型的方法,可以得到最大化这样一个目标函数:
$$
L = \sum_{s \in S} \sum_{l_i \in s}(\sum_{-m \leq j \leq m}\log P(l_{i+j}|l_i))
$$
其中
$$
P(l_{i+j} | l_i) = \frac{\exp(v^T_{l_i}v^{‘}_{l_{i+j}})}{\sum_{i=1}^V \exp(v^T_{l_i}v^{‘}_{l})}
$$
$v_l$和$v^{‘}l$分别是listing l的输入和输出表示。观察上式概率定义中的分母,它是关于所有的listing表示求和,在实际计算时,效率较低,所以论文中采用负采样的方法来解决这一问题。若使用负采样方法,则目标函数变为
$$
\max \sum{(l,c) \in D_p} \log \frac{1}{1+e^{-v_c^{‘}v_l}} + \sum_{(l,c) \in D_n} \log \frac{1}{1+e^{v_c^{‘}v_l}}
$$
其中$D_p$是被点击的l和它的上下文listing c 对组成的集合,$D_p$是被点击的l以及随机采样的c构成负采样集合,关于负采样的损失函数为什么是上式,可以参考[1], [2]。
被订购listing作为全局的context
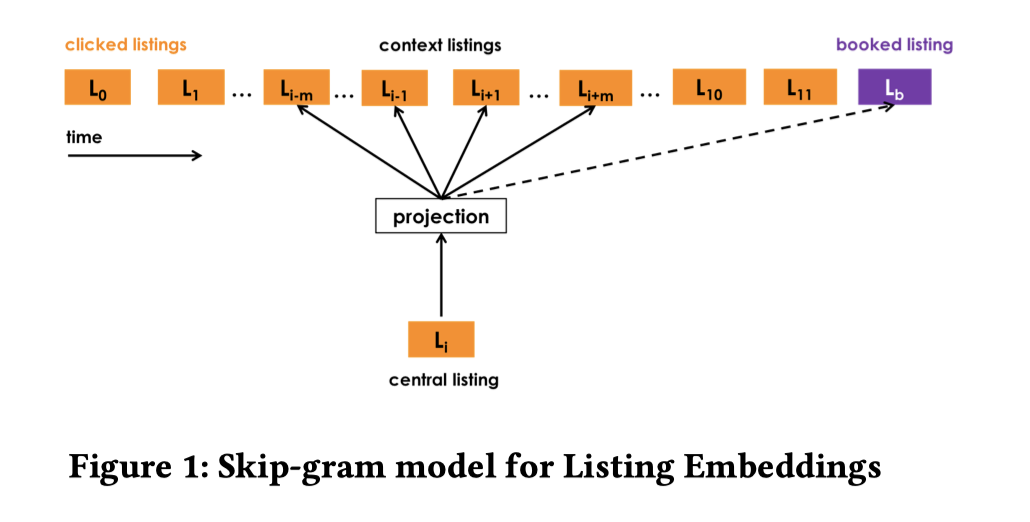
可以把被点击的listing分成两类,一类是点击并且被订购的listing,一类是只点击,并没有发生订购的listing。所以为了区分产生订购的序列和没有发生订购的序列,并且希望对于发生订购的序列能够学习出更好的嵌入表示,论文将订购的listing作为整个序列(有订购listing产生的序列)全局的context,即不管这个被订购的listing在不在中心listing的滑窗范围内,都把它当做中心listing的context。这样的话,对于产生订购行为的序列,目标函数变为:
$$
\max \sum_{(l,c) \in D_p} \log \frac{1}{1+e^{-v_c^{‘}v_l}} + \sum_{(l,c) \in D_n} \log \frac{1}{1+e^{v_c^{‘}v_l}} + \log \frac{1}{1+e^{-v_{lb}^{‘}v_l}}
$$
其中$v_{lb}$表示订购listing的嵌入表示。如下图所示表示了这一模型。
Adapting Training for congregated Search
在做采样时,$D_p$中包含的样本往往都是和中心listing在相同的城市或区域,而$D_n$中采样的样本是从所有的训练集中得到的,往往与中心listing不在一个区域,这样就引入了一定的偏差,为了缓解这一问题,论文中提出引入另一个负采样集合$D_{mn}$,它是由和中心listing在相同区域的负样本随机采样得到。这样的话损失函数就可以修改为:
$$
\max \sum_{(l,c) \in D_p} \log \frac{1}{1+e^{-v_c^{‘}v_l}} + \sum_{(l,c) \in D_n} \log \frac{1}{1+e^{v_c^{‘}v_l}} + \log \frac{1}{1+e^{-v_{lb}^{‘}v_l}} + \sum_{(l,mn) \in D_{mn}} \log \frac{1}{1+e^{-v_{mn}^{‘}v_l}}
$$
冷启动问题
对于新加入的新的listing,通过listing的基本信息计算与它相似的几个listing,然后利用与它相似的listing的embedding的平均值作为新的listing的embedding。
User-type和listing-type embedding
上面计算每个listing的embedding,通过embedding计算listing的相似性,可以用来度量用户的短期兴趣,即当用户点击了某个listing,可以实时地基于这个listing给用户推荐下一个listing。论文中提到希望能够基于用户过去订购的历史对用户的长期兴趣进行建模,但是存在几个问题:用户订购的样本远远的少于用户点击的样本、很多用户过去仅仅只有一个订单、用户两个订单之间往往相隔的时间跨度很大、学习一个有效的embedding这个listing往往需要至少在数据中出现5-10次。为处理数据稀疏性带来的问题,论文提出学习user-type和listing-type的embedding,而不是学习user—id和listing-id的embedding,所以论文就提出根据user和listing的属性性质使用一定的规则对user和listing进行聚类,这样每个user-type和listing-type就包含了多个样本在序列中。
为学习user-type和listing-type的embedding,论文采用了与上文所讲的类似的损失函数:
$$
\max \sum_{(ut,c) \in D_{book}} \log \frac{1}{1+e^{-v_c^{‘}v_{ut}}} + \sum_{(ut,c) \in D_{neg}} \log \frac{1}{1+e^{v_c^{‘}v_{ut}}}
$$
和
$$
\max \sum_{(lt,c) \in D_{book}} \log \frac{1}{1+e^{-v_c^{‘}v_{lt}}} + \sum_{(lt,c) \in D_{neg}} \log \frac{1}{1+e^{v_c^{‘}v_{lt}}}
$$
对房东拒绝订单建模
顾客订购了listing,但是有可能被房东拒绝掉,所以为了体现出这一特点,在损失函数中引入了一个和房东拒绝相关的项:
$$
\max \sum_{(ut,c) \in D_{book}} \log \frac{1}{1+e^{-v_c^{‘}v_{ut}}} + \sum_{(ut,c) \in D_{neg}} \log \frac{1}{1+e^{v_c^{‘}v_{ut}}}+\sum_{(ut,lt) \in D_{reject}} \log \frac{1}{1+e^{-v_{lt}^{‘}v_{ut}}}
$$
和
$$
\max \sum_{(lt,c) \in D_{book}} \log \frac{1}{1+e^{-v_c^{‘}v_{lt}}} + \sum_{(lt,c) \in D_{neg}} \log \frac{1}{1+e^{v_c^{‘}v_{lt}}}+\sum_{(ut,lt) \in D_{reject}} \log \frac{1}{1+e^{-v_{lt}^{‘}v_{ut}}}
$$
参考
[1] word2vec Explained: Deriving Mikolov et al.’s Negative-Sampling Word-Embedding Method
[2] word2vec 中的数学原理详解(五)基于 Negative Sampling 的模型
[3] Real-time Personalization using Embeddings for Search Ranking at Airbnb

